Reliability
Reliability is the degree to which a method provides estimates that are stable or consistent, as opposed to erratic or variable. It describes the extent to which a method is able to yield reproducible data under the various conditions or contexts for which it has been designed.
The following terms have been used often interchangeably with reliability in the literature [1,2]:
- Reproducibility
- Repeatability
- Replicability
- Consistency
- Stability
- Agreement
- Concordance
- Precision
The rule of thumb would be to describe what each means sufficiently in detail. Reliability is decreased by measurement error, most commonly random error, which causes estimated values to vary around the true value in an unpredictable way. It can arise from chance differences in the method, researcher or participant. Poor reliability weakens observed associations between exposure and outcome variables which can conceal true relationships between behaviour and disease [3,4]. It also results in misclassification when categorising data. Reliability is a concern for any method and determines the upper limit for validity.
Reliability is closely linked to validity, however while validity relates to the accuracy of a method, reliability relates to the consistency. It is therefore possible for a method with poor validity to be very reliable. For example, replicate measures using the same faulty tape might provide very similar, reliable, measurements of length, but would not be valid due to the underlying poor agreement with the true length.
The relationship between reliability and validity is described visually by the target example in Figure C.3.1. The above example is represented by the ‘reliable but not valid’ target.

Figure C.3.1 The relationship between reliability and validity at an individual level.
It is possible for a method to be unreliable at an individual level, but provide valid estimates at the group level using the mean, as shown by Figure C.3.2 below. Such a method would not be valid at an individual level.
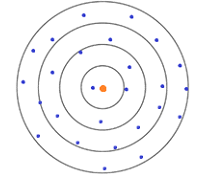
Figure C.3.2 Relationships between reliability and validity at group level. Not reliable and not valid at individual level, but valid at group level using mean of all values.
Test-retest reliability (also known as stability)
The extent to which a method produces consistent data in similar conditions across multiple time points. For example, fat mass assessed with an electronic device may vary due to random errors resulting from differences in calibration. To assess how reliable the test is, replicate assessments in the exact same setting can be undertaken.
Demonstrating this type of reliability may be problematic in the assessment of diet and physical activity due to the relatively high intra-individual variation of these variables. Some methods are likely to have particularly high day-to-day variation, e.g. 24-hour dietary or physical activity recall. Consideration should be given to the time between assessments when assessing test-retest reliability.
- For example, if maximal oxygen consumption was assessed repeatedly on the same day, measures would be expected to decline due to fatigue.
- Reliability could be deemed to be poor, but this would be a result of true variability in phenomenon rather than measurement error.
- On the other hand, measures on different days could involve a real change in physical fitness.
- It is often difficult to separate the test-retest reliability of the method from the instability of the true value over time.
Internal consistency reliability
- A measure of the extent to which items within a tool measure the same construct, or the consistency of a method across multiple applications within a single phase of a study.
- Commonly used in psychology, where multiple questions in a single questionnaire try to capture a single psychological ‘domain’ (e.g. temper).
- Can be measured using Cronbach’s alpha [5], which is expressed as a number between 0 and 1, with values closer to 1 indicating that items within a method are more related to each other.
- High scores do not indicate that the measure is unidimensional (this could be examined using exploratory factor analysis).
- This reliability can be obtained in a three-factor eating questionnaire in which multiple questions are asked to capture each of three domains of tendency or feeling in diet: "cognitive restraint of eating", ‘disinhibition’, and ‘hunger’.
Inter-rater reliability (also known as inter-rating agreement or concordance)
The similarity between data from different observers of the same phenomenon, for example, the concordance of:
- Data produced by two research assistants using the same method to observe the intensity of activity of children during physical education
- Ultrasound assessments of abdominal fat mass by two operators
- Two research assistants who estimated nutrient intakes from hand-written multiple-day weighed dietary records with digital photos of each meal
The degree of inter-rater reliability is particularly important when using methods that require a certain level of interpretation or observation by investigators. High inter-rater reliability indicates a good level of standardisation, whereas low inter-rater reliability indicates a high level of measurement error due to variability in subjective assessment.
Assessing reliability when measuring highly variable data
The choice of an appropriate method should always involve consideration of its ability to provide reliable data, and this can be tested in a reliability study. Reliability can be assessed in variables that remain stable over long periods, such as psychological traits, social attitudes, or height of an adult.
Diet and physical activity, on the other hand, are inherently variable on a day-to-day basis. There are consequently two main sources of variability which affect the reliability of a measurement:
- Random error associated with the method itself
- True variation or instability in human behaviour or characteristic (intra-individual variation)
It can be difficult or even impossible to distinguish between these components. An assessment of reliability relates the degree of measurement error to the underlying true variability in the variable:
- If reliability is high, the measurement error is small in comparison to the true variability.
- If reliability is low, the measurement error is high relative to the true variability.
Reliability for absolute or relative measures
Absolute changes in an individual’s behaviour or characteristics over time reduce reliability. However, even if absolute values of individuals’ characteristics change over time and are not reproducible, ranking or relative difference between individuals can be reproducible and reliable.
For example, growth curves are used to monitor the growth of a child or children:
- Repeated measures of the weight of a growing child are not reproducible over weeks, and thus absolute validity is poor.
- However, the measured value can be compared to a global average score standardised for sex and age.
- The relative difference between measured weight and globally standardised weight would likely be more repeatable than the absolute value.
Alternatively, physical activity may be assessed repeatedly throughout a six month period:
- The absolute values would demonstrate poor reliability due to well-established seasonal variation in activity levels.
- However, the ranking of individual physical activity levels within a cohort can be reliable over time (Figure C.3.3 below illustrates a hypothetical example).
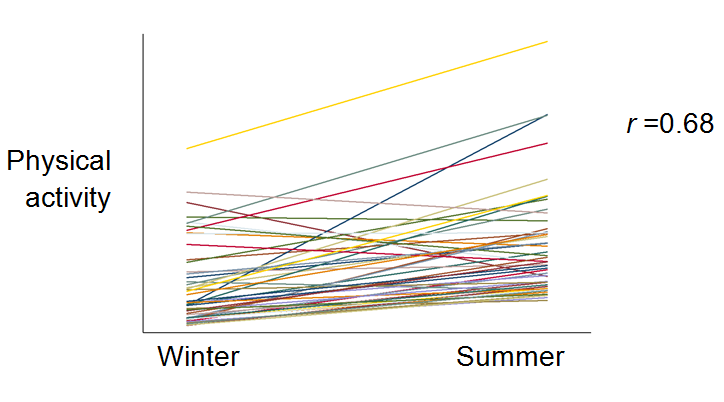
Figure C.3.3 Hypothetical example of the absolute and relative reliability of physical activity measure between winter and summer.
Reliability in a multi-centre study
- In a large-scale study on lifestyle and health, investigators often recruit study participants from multiple geographical areas through regional centres.
- If such a study is planned, on-site assessment should ideally be employed to standardise measurement across sites.
- In research adapting an imaging technique to perform anthropometry, for example, an imaging ‘phantom’ is used, mimicking target physics.
- If a blood biomarker is assayed in multiple laboratories, quality control samples are to be distributed to confirm how reproducible results are between laboratories.
- A study without this strategy would be subject to a critique about uncertainty without standardisation across different laboratories.
Reliability is a term loosely used in population-health sciences, due to lack of clarity surrounding repeatability of an instrument vs. variability of target characteristics over time. Ideally, a study should embark with a clear design in which different types of reliability of a method are accounted for, and with a (statistical) plan to assess them.
The level of method reliability that is required or desirable can vary by study. As such, it is essential to consider wider factors when evaluating reliability, such as:
- The characteristics of the sample used in the reliability study
- The scientific rigour of reliability study
- Variable or dimension of interest
- Time frame
- The study design being used to answer the research question
- Degree of absolute or relative reliability necessary
High reliability does not necessarily mean high validity
- A method may be highly reproducible and valid for the assessment of a variable, for example, body weight.
- However, this method is not valid to assess adiposity in a body, because body weight does not inform fat mass, lean mass, or location of fat deposition.
- This highlights the need to distinguish between systematic error and random error, as documented on the error and bias page.
Reliability affected by multiple non-biological effects
- Consideration about reproducibility is often needed in a prospective study using a biomarker (e.g. blood) to assess a blood nutrient, for example.
- Figure C.3.4 below indicates that four scenarios of two repeated measures can demonstrate different types of reproducibility.
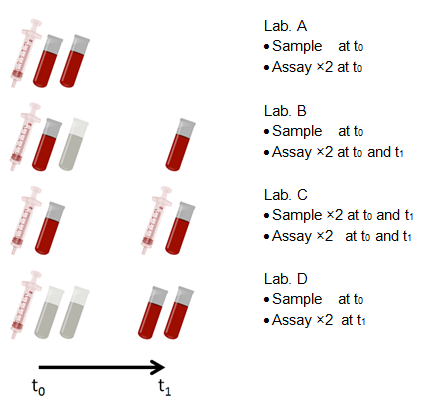
Figure C.3.4 Four scenarios demonstrating non-biological effects on the reliability of two repeated measures.
In the four different laboratories described in Figure C.3.4:
- Lab. A informs test-retest reliability of the assay at t0
- Lab. B informs reliability affected by two effects:
- Effect of blood storage between t0 and t1
- Effect of changes in lab. setting between t0 and t1
- Lab. C informs reliability affected by two effects:
- Effect of the temporal variation of study participants between t0 and t1
- Effect of changes in lab. setting between t0 and t1
- Lab. D informs test-retest reliability of the assay at t1 of which measures are affected by the effect* of blood storage between t0 and t1
Effects detrimental to reliability can be reduced by the proper application of quality control measures. For example, unwanted effects of blood storage can be corrected by measuring the effect and calibrating observed values accordingly.
The reliability of a diet, physical activity, or anthropometric method depends on the:
- The method itself
- Target behaviour or characteristic
- Time frame of the method
- Population and context of the study
- Inter- and intra-individual variation in the phenomenon
- Analytic methods
In order to increase the reliability of an assessment, the sources and types of error must be identified. A random error may be reduced by:
- Increasing the number of measurements taken per participant
- Increasing the sample size or the length of follow up in a cohort study
- Frequent calibration of instruments
- Incorporating quality control and assurance in the assessment process:
- Rigorous standard operating procedures
- Manual of procedures
- Standardised rigorous and consistent training of fieldworkers/interviewers undertaking assessments
- Inter- and intra-observer reliability checks
- Pilot studies, particularly if a new questionnaire is being designed.
- Bartlett JW, Frost C. Reliability, repeatability and reproducibility: analysis of measurement errors in continuous variables. Ultrasound Obstet Gynecol. 2008;31(4):466-75.
- Goodman S, Fanelli D, Ioannidis JPA, What does research reproducibility mean?, Sci Transl Med, 2016;8(341):341ps12
- Bennett DA, Landry D, Little J, Minelli C, Systematic review of statistical approaches to quantify, or correct for, measurement error in a continuous exposure in nutritional epidemiology, BMC Med Res Methodol, 2017;17:146
- Clayton D, Measurement error: effects and remedies in nutritional epidemiology, Proc Nutr Soc, 1994;53:37-42
- Tavakol M, Dennick R. Making sense of Cronbach's alpha. Int J Med Educ. 2011;2:53-5
